Group G: Pengfei Li, Ashton Henry, Annie Orukotan, kyuho chang, Hongsik kim
Section #1: Background Knowledge on Fractions
Instructor: Annie Orukotan
Students: Grade 3.
Age group: 7 – 8 years old
This lesson plan is objectively meant to act as a teachers guide for introducing students who are yet to encounter fractions in other lectures or classes.This lesson will build on already familiarised knowledge such as mathematical functions including addition, subtraction, division and multiplication. Existing understanding of these numerical functions play a critical role in students’ long run understanding of fractions and other continuing topics.
Objectives;
- Students will be able to identify fractions as part of a whole
- Students will be able to represent fractions visually using shapes.
- Students will be able to compare fraction
Materials needed; .
- Coloured pencils or markers
- Paper
- Shape cut outs (Including but not limited to circles, rectangles, and squares)
Firstly students should be asked questions such as;
- What are the different mathematical functions
- How can they be used?
This is important to assess students’ learning and understanding on the core prerequisite topic for fractions and other topics that will build upon the foundation topic of mathematical functions. To refresh students’ memory, the video below should be played and the question at the end should be answered.
I have decided on using the multimedia principle to allow adequate understanding of the background knowledge (mathematical functions). The multimedia principle states that humans learn best from words and picture rather than just words alone. The videos presented below allow for both visual and audio presentation of information, which students will find easier to comprehend and understand. Information on the mathematical functions such as addition and subtraction are shown in the videos with pictures, word, and audio interpretation of the visual information present in the videos. Although the topic of both addition, subtraction, multiplication and division have been previously introduced and taught to students using the multimedia principle allows students to refresh their memories on these topics.
Video 1: Multiplication & Division
Video 2: Adding & Subtraction
Section #2: Fraction Introduction
Instructor: Ashton Henry
This video I created aims to educate students on the topic of fractions from the 3rd grade ranging from 7-8 years old. Many choices I made were influenced by what we’ve learned in the course so far. Choices like the colors were important as I wanted them to contrast for easy-to-read sections so I chose white for the background and black for the text. I used what we learned on storytelling to hopefully kindle interest in fractions using my lesson with a story that could be seen as relatable. Another important part was relating to previous knowledge and asking them to see what they can notice in their own life would tie in knowledge to the outside world helping kindle a better understanding of the topic. Using the right imagery helps a lot due to the fact these are young students so keeping attention can be difficult. The tone I spoke with in the video was a bit more upbeat as you have to keep it light so as not to make students lose interest. Adding in the 2 questions can also help with engagement as it makes students think about what they’ve learned. Overall I believe the combination of all of these points allowed me to create an effective and engaging lesson
Section #3: How to Read and Write Fractions
Instructor: Hongsik Kim
Basic concept of fraction: A fraction is a mathematical representation of a part of a whole. It is written as a ratio of two numbers separated by a horizontal line. The number above the line is called the numerator, and the number below the line is called the denominator.
Let’s start from Writing Fraction!
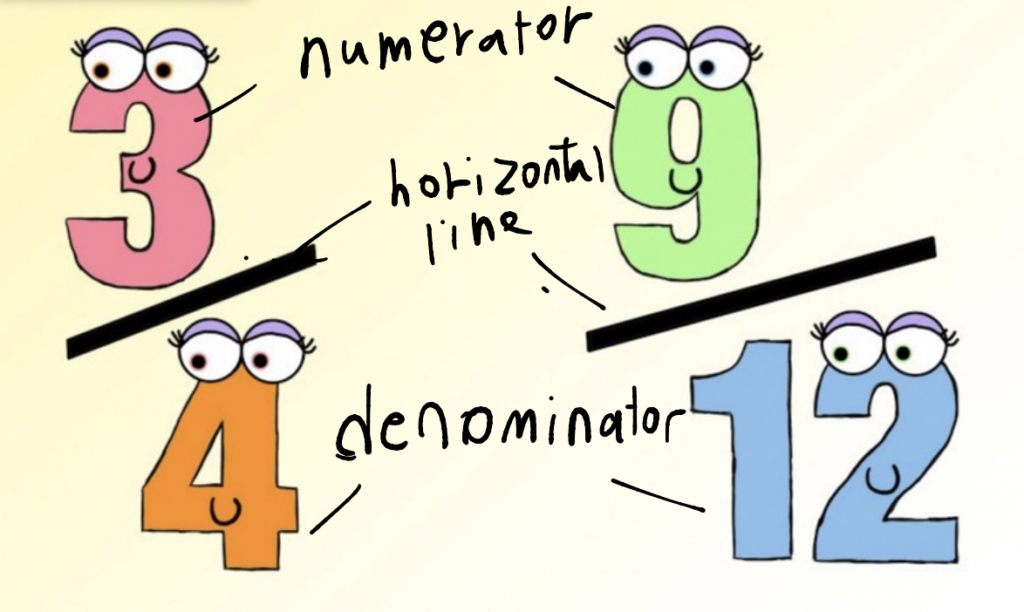
As a we look at the picture, we need 3 things for fraction. numerator, horizontal line and denominator.

There are 9 animals (4 cats and 5 dogs)
what is denomiator? 9! (4 cats +5dogs)
what is numerator of cats? 4!
what is numerator of dogs? 5!
For example, the fraction cat 4/9 represents 4 parts out of a total of 9 parts. The number 4 is the numerator, and the number 9 is the denominator.
I used one of the Managing Intrinsic Load principle which is segmenting. in the first picture by segmenting fraction in to 3 details . Segmenting is a common strategy used in instructional design to break down complex information or processes into smaller, more manageable pieces. By doing this, students can more easily understand and remember the information, and also have more control over their own learning pace. It’s a great way to help learners build their knowledge and skills step by step, and gradually increase their mastery of a topic.
How to read fractions!

point is reading numerator as a cardinal number, denomiator as a ordinal number.
A Cardinal Number is a number that says how many of something there are, such as one, two, three, four, five.
An Ordinal Number is a number that tells the position of something in a list, such as first second third fourth fifth etc.
Fractions can be used to represent parts of a whole, parts of a set, or parts of a measurement. They are commonly used in everyday situations, such as in cooking, where recipes often call for a certain amount of ingredients in fractions.

Fractions can be added, subtracted, multiplied, and divided just like whole numbers, but with some additional rules. To add or subtract fractions, the denominators must be the same. To multiply fractions, you multiply the numerators and denominators together. To divide fractions, you flip the second fraction and multiply it by the first fraction.This is why there are pre-request knowlege. More information is in annie’s section.
Also I used modality principle, reason for this is that when learners receive information through multiple modalities, they are able to process the information through both their visual and auditory channels, which can help them to better encode and retain the information.
Section #4: How to Compare Fractions
Instructor: kyuho chang
Comparing fractions is a key competency for pupils to develop in their mathematical studies. This involves understanding that fractions are a way of expressing parts of a whole. The numerator of a fraction signifies the number of parts, while the denominator represents the total number of parts in the whole.
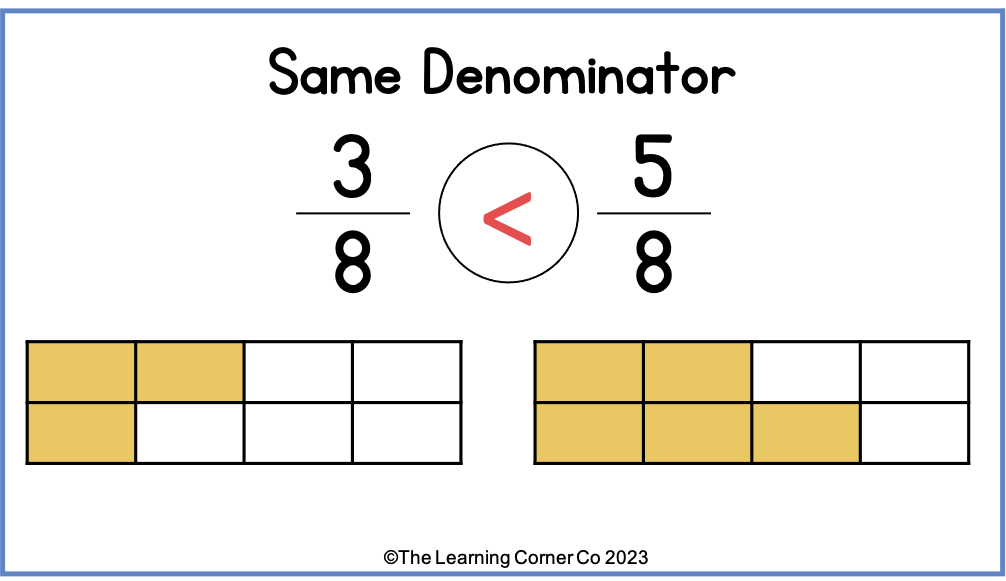
When comparing fractions with the same denominator, students need to simply evaluate the numerators. Whichever numerator is greater signifies the greater fraction. For instance, if we have the fractions 3/8 and 5/8, we can see that 5/8 is greater than 3/8 due to the larger numerator.
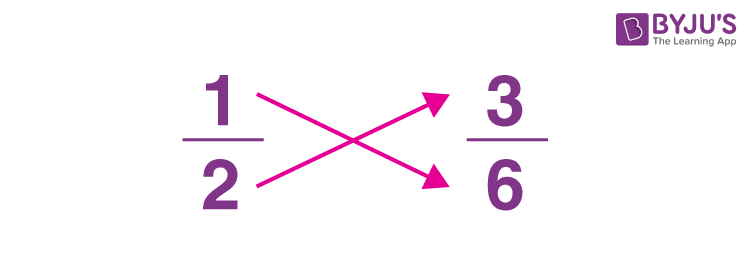
Comparing fractions with distinct denominators can be a little more tricky, but can be done by obtaining a common denominator. This can be achieved by finding the least common multiple of the two denominators. After obtaining a common denominator, they can convert the fractions to equivalent fractions with the same denominator and compare the numerators.
Equivalent fractions are also a significant concept for students to understand. Equivalent fractions are those that represent the same part of a whole but are written differently. For example, 1/2 and 3/6 are equivalent fractions because they both represent half of a whole.
By mastering the skill of comparing fractions, students will be able to solve a broad range of problems involving fractions, such as ordering fractions, adding and subtracting fractions, and solving fraction word problems.
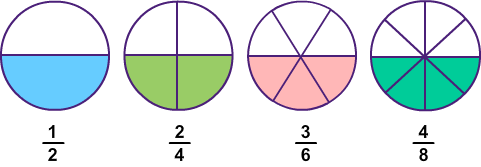
Section #5: In-Class Activities
Instructor: Pengfei Li (Jasper)
Goal: To familiarize students with what they learned during the lecture.
Design Rationale:
My audiences are grade 3 elementary school students whose age are around 7 to 8. Students at this age are energetic and curious. They are typically eager to learn and explore the world around them. In this case, using multiple questions or any other text-only media cannot attract them properly. Thus, I choose to use playcards, audio voice tests, and ranking activities to test their learning outcomes in understanding, reading and comparing respectively.
In this section, I will use the principles we learned in the active learning section. The activity design frame is mainly based on Bloom’s Taxonomy at the “apply” level. Students have already learned all the necessary skills in the previous sections. They can explore the interactive contents freely below with active learning attitudes. Noticed that the first playcards game also reflects Merrill’s First Principles. Images all reflect their daily life, and the last playcard also includes a real-world problem.
In-Class Activity #1: Playcards Game
In-Class Activity #2: Reading Game
(Alert: To play with this section, you should use Google Chrome as the browser)
In-Class Activity #3: Comparison Game